
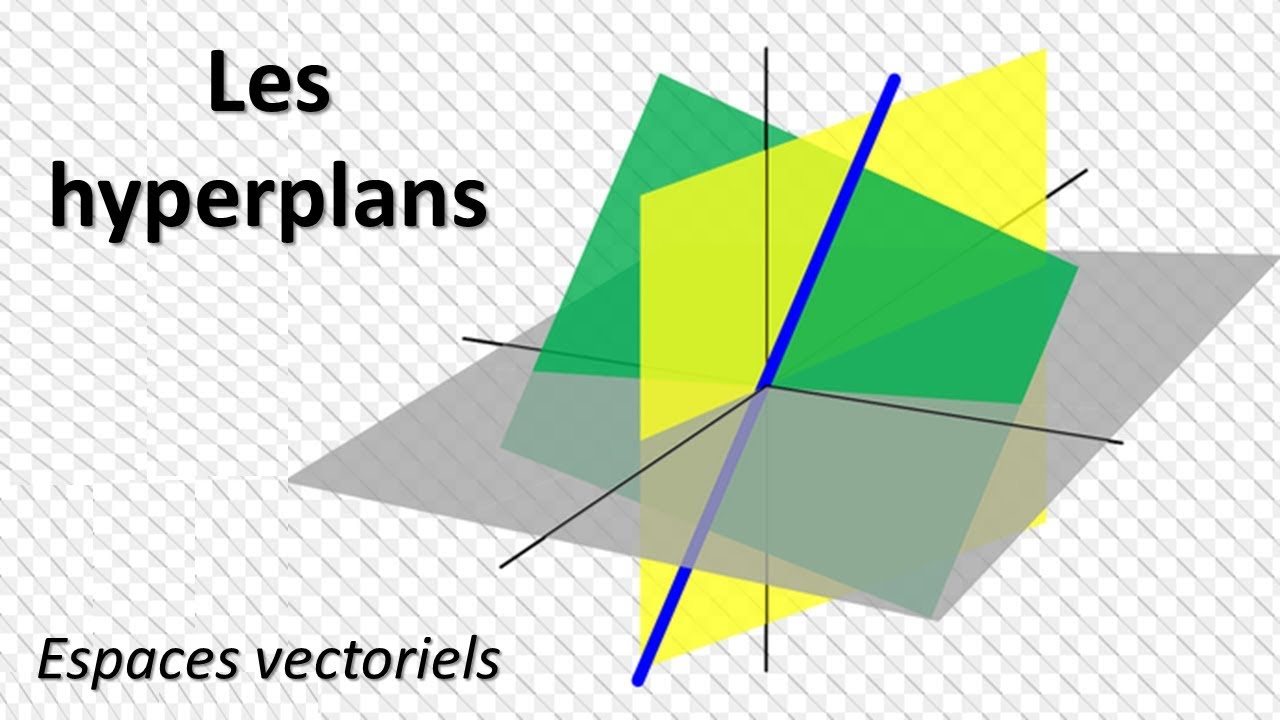

It doesn’t perform very well when the dataset has more noise, i.e.SVMs do not directly provide probability estimates-these are calculated using an expensive five-fold cross-validation process (see scores and probabilities, below).The same set of parameters will not work optimally for all use cases. Then they can be exhausted by sequences of compact, convex subsets An and Bn. For the second version of the theorem, suppose that A and B are disjoint, convex, and open. The main disadvantage of SVM is that it has several key parameters like C, kernel function, and Gamma that all need to be set correctly to achieve the best classification results for any given problem. Then any hyperplane H which is perpendicular to the segment I ( p, q) from p to q, and which meets the interior of this segment, must separate A from B.It works really well with a clear margin of separation.In Cartesian coordinates, such a hyperplane can be described with a single linear equation of the following form (where at least one of the s is non-zero): In the case of a real affine space, in other words when the coordinates are real numbers, this affine space. parameters from svmStruct w1 dot (svmStruct.Alpha, svmStruct.SupportVectors (:,1)) w2 dot (svmStruct.Alpha, svmStruct.SupportVectors (:,2)) bias svmStruct.Bias y ax + b a -w1/w2 b -svmStruct.Bias/w2. An affine hyperplane is an affine subspace of codimension 1 in an affine space. Common kernels are provided, but it’s also possible to specify custom kernels. Just call the svmStrain function with autscale on false. SVM is versatile: different kernel functions can be specified for the decision function.
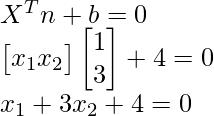
It’s still effective in cases where the number of dimensions is greater than the number of samples.Is is usually built from the combination of a point and a vector and it corresponds to a n 1 dimensional vector. It’s very effective in high-dimensional spaces as compared to algorithms such as k-nearest neighbors. 1.2 Hyperplane equations To de ne the hyperplane equation we need either a point in the plane and a unit vector orthogonal to the plane, two vectors lying on the plane or three coplanar points (they are contained in the hyperplane).However, by using a nonlinear kernel as mentioned in the scikit-learn library, we can get a nonlinear classifier without transforming the data or doing heavy computations at all. Normally, the kernel is linear, and we get a linear classifier. The only difference is that we have the hinge-loss instead of the logistic loss.įigure 2: The five plots above show different boundary of hyperplane and the optimal hyperplane separating example data, when C=0.01, 0.1, 1, 10, 100.Different kernel functions applied on Iris-Dataset Setting: We define a linear classifier: $h(\mathbf,b$) just like logistic regression (e.g. Here b is used to select the hyperplane i.e perpendicular to the normal vector. These are commonly referred to as the weight vector in machine learning. A separating hyperplane can be defined by two terms: an intercept term called b and a decision hyperplane normal vector called w. The SVM finds the maximum margin separating hyperplane. Below is the method to calculate linearly separable hyperplane. The Perceptron guaranteed that you find a hyperplane if it exists. The Support Vector Machine (SVM) is a linear classifier that can be viewed as an extension of the Perceptron developed by Rosenblatt in 1958.


 0 kommentar(er)
0 kommentar(er)
